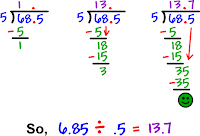LOS NÚMEROS DECIMALES

   Antes que nada el creador de los números decimales fue el científico Simón Stevin (548-620). Nacido en Brujas, ciudad de Bélgica.

   El origen de los números decimales nace como uina forma especial  de escritura de las fracciones decimales, la cual lo coma separa la parte entera de la parte decimal y si no hay enteros se coloca un cero delante (lado izquierda) de la coma.

   Por ejemplo:

3/10 = 0,3                     8743/1000 = 8,743  

57/100 =  0,57              3278/1000000 = 0,003278

   La parte decimal tiene columnas de posición, determinados por el denominador de cada fracciòn decimal.

8(parte entera),743(parte decimal)

Entonces:

• Los décimos-denominador 10, ocupan 1 lugar después de la coma.
• Los centésimos-denominador 100, ocupan 2 lugar después de la coma.
• Los milésimos-denominador 1000, ocupan 3 lugares después de la coma y así sucesivamente.

   Por lo tanto en los nùmeros decimales, los lugares se relacionan con la cantindad de ceros que tiene la potencia de 10 del denominador. Y la última cifra del numerador de la fracción decimal debe ocupar la posición que indica el denominador y si no llegase alcanzar las cifras dadas se coloca un cero a la izquierda de ellas.

SUMA CON DECIMALES

   Para sumar los números decimales se colocan alineando las comas y de tal forma que se alinen unidades con unidades, decenas con decenas, centenas con centenas y después la coma (derecha) décimas con décimas, centésimas con centésimas y así sucesivamente. Y en seguida se realiza la suma y al finalizar se pone la coma en línea con las de los sumandos.

RESTA CON DECIMAL

   En cuanto a la resta al igual que la suma; se acomodan en columnas alienando las comas, sin embargo, la cantidad grande se coloca primero que la menor en la resta.

MULTIPLICACIÓN CON DECIMAL

   Para la multiplicación se coloca los números en columnas igualados por la derecha pero ahora sin importar la alineación de las comas, se realiza la operación y al final se coloca la coma en el producto los lugares que separe tantas cifras decimales comotuvieron los dos factores juntos.

DIVISÓN CON MULTIPLICACIÓN

   Antes se debe revisar si hay comas y si es así como quiera se realiza la operación. Para ello se desplaza las comas a la derecha en el dividendo y en el divisor el mismo número de puestos, y se lleva acabo la operación.

Números decimales from Hugo EA-Garza

FRACCIONES

   Fracción es un número que se obtiene de dividir una totalidad en partes iguales.

   Pero antes que nada las matemáticas se entiende como un medio para aprender y resolver problemas, en la cual se busca en los alumnos desarrollen actitudes así mismo utilicen estrategias en donde les permitan desarrollar capacidades para comprender y para poder solucionar los problemas.

   Sin embargo cuando se trata de explicar a los alumnos estos presentan algunas dificultades que van desde: No existe una noción de reparto y no comprenden la función del numerador y denominador.

   Siendo dificultades también para el mismo docente para poder enseñar las fracciones, sin embargo,  para poder enseñar los conceptos, problemas a utilizar que estos sean acorde o vinculados al lenguaje cotidiano (vida cotidiana), es decir, que sean acercadas a los alumnos para poder comprender. Para lo cual un profesor al tratar de afirmar en los estudiantes el concepto de fracción, se recomienda utilizar diversos objetos para ir estructurando detenidamente los conceptos.

A manera de sugerencia didáctica los principios que deben regir la enseñanza de las fracciones según L. Streefland son:

• Lo importante es que los propios niños construyan las operaciones con fracciones. Construcción que debe basarse en las propias actividades del alumno como: estimación, desarrollo del sentido del orden y tamaño.

• Valorar las actividades de los alumnos, así como los métodos y procedimientos que utilicen para resolver los problemas, aunque difiere de la formalidad propia de la materia.

• Que el alumno sea capaz de formular sus propias reglas y generalizaciones para adquirir sus conocimientos.

• Se deben utilizar los saberes previos del alumno como base para empezar la secuencia de la enseñanza de fracciones.

   Aunque los maestros tienen que buscar elementos que les permitan facilitar y ejercitar las fracciones; como libros y actividades apropiadas para que los alumnos puedan comprender. Aun así el profesor debe estar consciente de que los conceptos matemáticos son entes abstractos.

   Los números racionales se expresan de dos formas: Fracciones y con notación decimal. Fracciones tiene su origen en las relaciones entre la aritmética decimal. El uso particular de fracciones decimales y su utilización para la medida de magnitudes, como el tiempo da lugar a la notación decimal.

   Tal como lo indica Llinares y Sánchez las fracciones pueden representarse de manera; geométrica, discreta, numérica y literal. Geométrica se realizan en un contexto continuo; los diagramas circulares, rectangulares y la recta numérica. La representación numérica se encuentran distintas formas de utilizar los números para indicar una relación parte-todo; representación como una división indicada 3/5, como razón 3:5, decimal 0,6 y representación literales; tres quintos, tres de cinco y proporción de tres a cinco.

     Según Moisés Coriat, las fracciones se expresan de formas sintética, tres formas de representación de las fracciones: con cifras, con palabras y mediante magnitudes.

Fracciones from Hugo EA-Garza